Estimating the circumference of the Earth (Posidonius)
Activity objectives
Background
Posidonius (135 - 51 BCE) was a Greek polymath born in the city of Apamea, in modern day Syria. He was acclaimed to be the greatest polymath of his time. At some point in his life, he settled in the Greek island of Rhodes, a famous scientific and cultural center. Posidonius spent many years in travel and scientific research in several European lands. Amongst other endeavors, he tried to explain the origin of tides, provided estimations for the distances of the Moon and Sun and, like Eratosthenes, calculated the size of the Earth; it is the latter of his efforts that we shall investigate.
- Learn about Posidonius a great polymath of antiquity
- Use simple geometric methods to estimate the circumference of the Earth
- Use Stellarium to replicate the measurement of the circumference of the Earth
- Become aware of the errors and limitations of the method of Posidonius
Background
Posidonius (135 - 51 BCE) was a Greek polymath born in the city of Apamea, in modern day Syria. He was acclaimed to be the greatest polymath of his time. At some point in his life, he settled in the Greek island of Rhodes, a famous scientific and cultural center. Posidonius spent many years in travel and scientific research in several European lands. Amongst other endeavors, he tried to explain the origin of tides, provided estimations for the distances of the Moon and Sun and, like Eratosthenes, calculated the size of the Earth; it is the latter of his efforts that we shall investigate.
Posidonius: Taken from Sailko / CC BY (https://creativecommons.org/licenses/by/3.0)
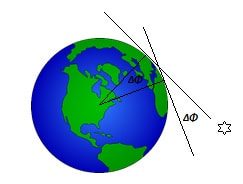
Posidonius calculated the Earth's circumference by observing the position of the bright star Canopus. He observed that the star could be viewed on, but never above, the horizon at Rhodes, while at Alexandria he saw it emerge clearly above the horizon. By assuming (as he thought) that Rhodes was 5,000 stadia due north of Alexandria (on the same meridian), he was able to estimate the circumference of the Earth as follows: The difference in the altitude of Canopus as viewed from two locations on the same meridian, is equal to the difference in the latitudes of the two locations. Once the difference in latitudes Δφ is obtained, the formula employed by Eratosthenes can be used to find the circumference of the Earth:
L/S = 360/Δφ
Posidonius calculated the Earth's circumference by observing the position of the bright star Canopus. He observed that the star could be viewed on, but never above, the horizon at Rhodes, while at Alexandria he saw it emerge clearly above the horizon. By assuming (as he thought) that Rhodes was 5,000 stadia due north of Alexandria (on the same meridian), he was able to estimate the circumference of the Earth as follows: The difference in the altitude of Canopus as viewed from two locations on the same meridian, is equal to the difference in the latitudes of the two locations. Once the difference in latitudes Δφ is obtained, the formula employed by Eratosthenes can be used to find the circumference of the Earth:
L/S = 360/Δφ
Method of Posidonius for estimation of the circumference of the Earth
Implementation in Stellarium
Start Stellarium and in the Date/Time Window, set the date to: -99 / 1 / 1 (any other day when Canopus is visible by night will do).
Also, since the observations for this experiment were made at seaports, using the Sky and Viewing Options Window, set the Landscape to 'Ocean' to add realism to the simulation. This will also make it easier to view the star Canopus as it appears just above the horizon.
Next, set the location in the Location Window to Alexandria in Egypt and note the latitude. Set the local time to 11 pm and find the maximum altitude of Canopus (i.e. when it is exactly South with an azimuth of 180 degrees).
Next, set the location to Rodos (Rhodes) in Greece and perform the same measurement.
Use the difference in the two altitudes (and therefore the two latitudes) to estimate the circumference of the Earth in stadia and in kilometers. Compare to the actual circumference of the Earth and comment on possible sources of error.
One source of error is caused by the diffraction of the light emitted by Canopus, i.e. the bending of the light due to the presence of the atmosphere. The diffraction of light will make stars appear at a higher position than they are at in reality.
Repeat the previous procedure and determine the actual altitude of Canopus in both Alexandria and Rhodes. For both cases have the atmosphere removed so that no diffraction of the light occurs. To do this you should use the relevant icon at the bottom of the screen or press the ‘a’ key.
Calculate the circumference of the Earth using your new values for the altitude of Canopus and compare your result to the one obtained previously. Also comment on the effect of diffraction on the position of Canopus in Alexandria and Rhodes. For which of the two locations is the effect greatest and why is this the case?
Implementation in Stellarium
Start Stellarium and in the Date/Time Window, set the date to: -99 / 1 / 1 (any other day when Canopus is visible by night will do).
Also, since the observations for this experiment were made at seaports, using the Sky and Viewing Options Window, set the Landscape to 'Ocean' to add realism to the simulation. This will also make it easier to view the star Canopus as it appears just above the horizon.
Next, set the location in the Location Window to Alexandria in Egypt and note the latitude. Set the local time to 11 pm and find the maximum altitude of Canopus (i.e. when it is exactly South with an azimuth of 180 degrees).
Next, set the location to Rodos (Rhodes) in Greece and perform the same measurement.
Use the difference in the two altitudes (and therefore the two latitudes) to estimate the circumference of the Earth in stadia and in kilometers. Compare to the actual circumference of the Earth and comment on possible sources of error.
One source of error is caused by the diffraction of the light emitted by Canopus, i.e. the bending of the light due to the presence of the atmosphere. The diffraction of light will make stars appear at a higher position than they are at in reality.
Repeat the previous procedure and determine the actual altitude of Canopus in both Alexandria and Rhodes. For both cases have the atmosphere removed so that no diffraction of the light occurs. To do this you should use the relevant icon at the bottom of the screen or press the ‘a’ key.
Calculate the circumference of the Earth using your new values for the altitude of Canopus and compare your result to the one obtained previously. Also comment on the effect of diffraction on the position of Canopus in Alexandria and Rhodes. For which of the two locations is the effect greatest and why is this the case?