Estimating the size of the Moon (Aristarchus)
Activity objectives
Background
Aristarchus also used his geometrical and astronomical knowledge to estimate the relative size of the Moon compared to that of the Earth. To do this he observed a lunar eclipse.
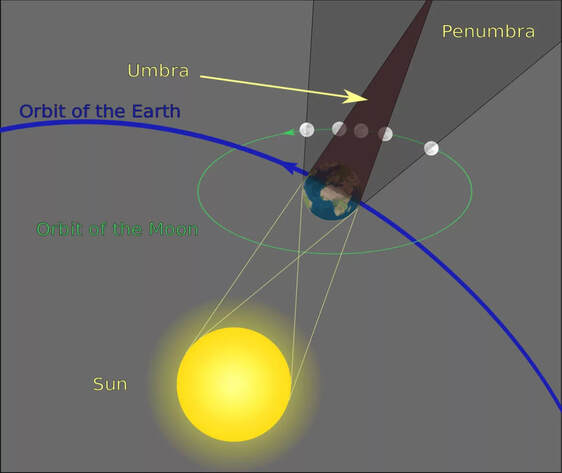
The geometry of a lunar eclipse is shown in the following figure. When the Sun - Earth - Moon are aligned, the Moon will move through the dark shadow of the Earth. If the alignment is such that the Moon becomes totally submerged in the dark shadow (known as umbra) then we witness a total lunar eclipse.
- Obtain an understanding of lunar eclipses
- Use the timings of a lunar eclipse to estimate relative size of the Moon
- Use Stellarium to replicate the measurement of the relative size of the Moon
- Become aware of the errors and limitations of the eclipse timing method
Background
Aristarchus also used his geometrical and astronomical knowledge to estimate the relative size of the Moon compared to that of the Earth. To do this he observed a lunar eclipse.
The geometry of a lunar eclipse is shown in the following figure. When the Sun - Earth - Moon are aligned, the Moon will move through the dark shadow of the Earth. If the alignment is such that the Moon becomes totally submerged in the dark shadow (known as umbra) then we witness a total lunar eclipse.
Geometry of lunar eclipse: Taken from http://www.planetary.org/multimedia/space-images/charts/geometry-of-a-lunar-eclipse.html
Aristarchus realised that by investigating the motion of the Moon in the Earth’s shadow he could estimate its relative size. We do not know for certain how exactly he did this but one method, and quite possibly the one he used, would be to measure the various timings of the eclipse.
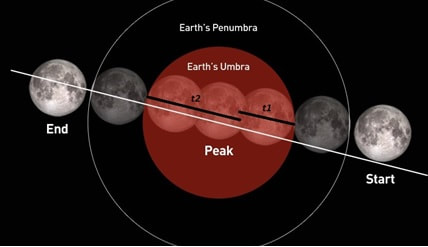
With this method, you start by estimating the duration of time between the moment when the edge of the Moon first became eclipsed and the moment when the Moon was first totally obscured (let’s call this t1). You can then measure the time duration for which the Moon was totally eclipsed (i.e. before it started to emerge from the Earth’s shadow), let’s call this t2.
To better understand the meanings of t1 and t2, have a look at the diagram below. Please note that the images of the Moon and the Earth’s shadow (umbra) are not portrayed exactly to scale, so you should not take into account the relative sizes shown in this diagram when taking your own measurements.
Aristarchus realised that by investigating the motion of the Moon in the Earth’s shadow he could estimate its relative size. We do not know for certain how exactly he did this but one method, and quite possibly the one he used, would be to measure the various timings of the eclipse.
With this method, you start by estimating the duration of time between the moment when the edge of the Moon first became eclipsed and the moment when the Moon was first totally obscured (let’s call this t1). You can then measure the time duration for which the Moon was totally eclipsed (i.e. before it started to emerge from the Earth’s shadow), let’s call this t2.
To better understand the meanings of t1 and t2, have a look at the diagram below. Please note that the images of the Moon and the Earth’s shadow (umbra) are not portrayed exactly to scale, so you should not take into account the relative sizes shown in this diagram when taking your own measurements.
Timings of lunar eclipse: Adapted from: https://www.theweathernetwork.com/news/articles/july-total-lunar-eclipse-is-the-longest-for-the-next-century-due-to-quirk-of-physics/106053
Simple logic can be used to deduce the formula:
Rs = (t2/t1)+1
where Rs is the relative size of the breadth of the Earth’s shadow with respect to the diameter of the Moon (i.e. how many times larger than the Moon the Earth’s shadow is). So, for example, if t2 = t1 then the breadth of the Earth’s shadow is double the diameter of the Moon.
Now an important point to make is that in this example, is that this corresponds to the Earth’s radius being double the radius of the Moon only if the shadow has a constant width. As we can see in the eclipse geometry figure this is not the case; in fact the shadow tapers (narrows) as we move away from the Earth. So for a better approximation we must multiply our result by a certain factor. Using geometrical calculations, this factor turns out to be roughly 1.35. So in this case, the radius of the Earth would have actually been estimated to be 1.35 x 2 = 2.7 times the radius of the Moon.
Implementation in Stellarium
Start Stellarium and in the Time/Date Window, set the date to:
-286 / 5 / 19.
This is when a long lunar eclipse occurred during Aristarchus’s time. The longer the lunar eclipse lasts for, the better the Sun, Earth and Moon are aligned, and the better the measurements that can be made.
Next, set the location in the Location Window to Athens in Greece. Set the local time to around 11:10 pm.
You must now look closely at the Moon, to do this you should click on it and then press the Page Up key to zoom in. Progress the time until you observe the beginning of the lunar eclipse. During a total lunar eclipse, the Moon does not vanish (like the Sun does in a total solar eclipse) but noticeably changes colour, becoming red. For a nice animation of this, click here!
Measure the times t1 and t2. Use the expression:
Rs = 1.35*[(t2/t1)+1]
to estimate the ratio of the radius of the Earth to that of the Moon. Compare to the result accepted nowadays and comment on possible sources of error. By assuming that the radius of the Earth is 6,371 km, estimate the actual radius of the Moon.
As viewed from the Earth, the Moon’s angular size is approximately 0.5 degree. Can you use this information and the value calculated for the radius of the Moon to find the distance of the Moon from the Earth? (Hint: You can use the small angle approximation!). Combine your result with the previous activity to obtain the distance of the Sun from the Earth in kilometers.
Simple logic can be used to deduce the formula:
Rs = (t2/t1)+1
where Rs is the relative size of the breadth of the Earth’s shadow with respect to the diameter of the Moon (i.e. how many times larger than the Moon the Earth’s shadow is). So, for example, if t2 = t1 then the breadth of the Earth’s shadow is double the diameter of the Moon.
Now an important point to make is that in this example, is that this corresponds to the Earth’s radius being double the radius of the Moon only if the shadow has a constant width. As we can see in the eclipse geometry figure this is not the case; in fact the shadow tapers (narrows) as we move away from the Earth. So for a better approximation we must multiply our result by a certain factor. Using geometrical calculations, this factor turns out to be roughly 1.35. So in this case, the radius of the Earth would have actually been estimated to be 1.35 x 2 = 2.7 times the radius of the Moon.
Implementation in Stellarium
Start Stellarium and in the Time/Date Window, set the date to:
-286 / 5 / 19.
This is when a long lunar eclipse occurred during Aristarchus’s time. The longer the lunar eclipse lasts for, the better the Sun, Earth and Moon are aligned, and the better the measurements that can be made.
Next, set the location in the Location Window to Athens in Greece. Set the local time to around 11:10 pm.
You must now look closely at the Moon, to do this you should click on it and then press the Page Up key to zoom in. Progress the time until you observe the beginning of the lunar eclipse. During a total lunar eclipse, the Moon does not vanish (like the Sun does in a total solar eclipse) but noticeably changes colour, becoming red. For a nice animation of this, click here!
Measure the times t1 and t2. Use the expression:
Rs = 1.35*[(t2/t1)+1]
to estimate the ratio of the radius of the Earth to that of the Moon. Compare to the result accepted nowadays and comment on possible sources of error. By assuming that the radius of the Earth is 6,371 km, estimate the actual radius of the Moon.
As viewed from the Earth, the Moon’s angular size is approximately 0.5 degree. Can you use this information and the value calculated for the radius of the Moon to find the distance of the Moon from the Earth? (Hint: You can use the small angle approximation!). Combine your result with the previous activity to obtain the distance of the Sun from the Earth in kilometers.