Determining the direction to Mecca
Activity objectives
Background
Over 1,000 ago, when Europe was in what is known as the Dark Ages and scientific thought in the region declined, it was in the Islamic empire where scientific knowledge flourished. At its peak this empire stretched from modern day Afghanistan in the East, to Spain and Portugal in the West. Astronomy was one of the sciences where many advancements were made, with Islamic scholars designing impressive new astronomical instruments and refining measurements and theories of other civilisations such as the Greeks and Indians, thus leading the way to a revolution in astronomy which took place in Europe a few hundred years later. The names of Ibn Yunus, Al Biruni or Nasir al-Din al-Tusi may not mean much to most people but their contribution to the development of astronomy was hugely significant.
- Learn about the achievements of medieval Islamic astronomers
- Gain an understanding of the connection of astronomy to the Islamic religion
- Use astronomical observations and mathematical formulae to determine the direction from a given location to Mecca
- Use Stellarium to replicate the determination of the direction to Mecca
Background
Over 1,000 ago, when Europe was in what is known as the Dark Ages and scientific thought in the region declined, it was in the Islamic empire where scientific knowledge flourished. At its peak this empire stretched from modern day Afghanistan in the East, to Spain and Portugal in the West. Astronomy was one of the sciences where many advancements were made, with Islamic scholars designing impressive new astronomical instruments and refining measurements and theories of other civilisations such as the Greeks and Indians, thus leading the way to a revolution in astronomy which took place in Europe a few hundred years later. The names of Ibn Yunus, Al Biruni or Nasir al-Din al-Tusi may not mean much to most people but their contribution to the development of astronomy was hugely significant.
Islamic Astronomers at Work: Taken from https://en.wikipedia.org/wiki/Astronomy_in_the_medieval_Islamic_world#/media/File:Taqi_al_din.jpg
So why was it that astronomy, of all sciences, experienced such great development in the Islamic world? An important driver for this interest in the skies lay in the Islamic religion itself. Significant religious events were regulated by the dynamics of celestial objects. For example, the start of a month in the Islamic calendar is determined by the first observation of the new moon crescent This is especially important for the month of Ramadan when those who practice the Muslim religion will fast. Furthermore, when praying, Muslims must face in the direction of the city of Mecca (more specifically that of the Kaaba, also spelled Ka'bah, a building at the center of Islam's most important mosque, the Great Mosque of Mecca), a direction known as the qibla. Islamic astronomers used mathematical tools together with measurements from lunar eclipses to determine this direction for several geographical locations. Finally, the prayer times for Muslims are determined by the position of the Sun in the sky, as it is the shadow cast by a gnomon (a vertical rod) that informs the faithful of when to perform each prayer.
We will start our journey into the wonders of medieval Islamic astronomy by seeing how those scholars determined the direction to their holy city.
Determining the direction to Mecca
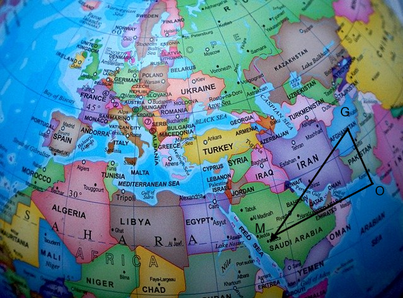
To determine the direction to Mecca from a specific location, one most solve the problem illustrated in the following diagram.
So why was it that astronomy, of all sciences, experienced such great development in the Islamic world? An important driver for this interest in the skies lay in the Islamic religion itself. Significant religious events were regulated by the dynamics of celestial objects. For example, the start of a month in the Islamic calendar is determined by the first observation of the new moon crescent This is especially important for the month of Ramadan when those who practice the Muslim religion will fast. Furthermore, when praying, Muslims must face in the direction of the city of Mecca (more specifically that of the Kaaba, also spelled Ka'bah, a building at the center of Islam's most important mosque, the Great Mosque of Mecca), a direction known as the qibla. Islamic astronomers used mathematical tools together with measurements from lunar eclipses to determine this direction for several geographical locations. Finally, the prayer times for Muslims are determined by the position of the Sun in the sky, as it is the shadow cast by a gnomon (a vertical rod) that informs the faithful of when to perform each prayer.
We will start our journey into the wonders of medieval Islamic astronomy by seeing how those scholars determined the direction to their holy city.
Determining the direction to Mecca
To determine the direction to Mecca from a specific location, one most solve the problem illustrated in the following diagram.
Estimation of the qibla direction
As can be seen, if the difference in latitudes between our location (in this case the city of Ghazni in Afghanistan) and Mecca is Δφ and the difference in longitude is Δλ, those can be used to find the angle OGM which essentially gives us he direction of the qibla.
Early Islamic astronomers used crude approximations to do this. They assumed that the triangle OGM is a right - hand planar triangle (i.e. with all sides sitting on the same plane). In this case the tangent of the angle OGM will be equal to Δλ/Δφ and the direction to Mecca is easily determined. Therefore, the formula for the qibla as measured from the North would be:
q = arctan(Δλ/Δφ)
It is evident, however, that due to the spherical shape of the Earth, this is a crude approximation that will only give approximate results. So, from the 9th century CE, Islamic scholars improved methods originally proposed by the ancient Greeks to advance the field of spherical trigonometry that enables the determination of angles and distances on a spherical surface.
As can be seen, if the difference in latitudes between our location (in this case the city of Ghazni in Afghanistan) and Mecca is Δφ and the difference in longitude is Δλ, those can be used to find the angle OGM which essentially gives us he direction of the qibla.
Early Islamic astronomers used crude approximations to do this. They assumed that the triangle OGM is a right - hand planar triangle (i.e. with all sides sitting on the same plane). In this case the tangent of the angle OGM will be equal to Δλ/Δφ and the direction to Mecca is easily determined. Therefore, the formula for the qibla as measured from the North would be:
q = arctan(Δλ/Δφ)
It is evident, however, that due to the spherical shape of the Earth, this is a crude approximation that will only give approximate results. So, from the 9th century CE, Islamic scholars improved methods originally proposed by the ancient Greeks to advance the field of spherical trigonometry that enables the determination of angles and distances on a spherical surface.
Al Biruni: Taken from https://he.wikipedia.org/wiki/%D7%A7%D7%95%D7%91%D7%A5:Biruni_1.jpg
Many scholars worked on this problem, including one of the most prominent scientists of that era, the Iranian Abu Rayhan al-Biruni (973 – after 1050 CE). Al – Biruni studied almost all fields of science including mathematics, physics and astronomy. One of his most important works was the “Taḥdid nihāyāt al-amākin li-taṣḥīḥ masāfāt al-masākin” (“Determination of the Coordinates of Places for the Correction of Distances Between Cities”). In it he detailed all that one needed to know about determining longitudes and latitudes on land and provided a novel solution for determining the circumference of the Earth. He also came up with ingenious solutions to the spherical trigonometric problem of determining the direction of Mecca from Ghazni, the city in Afghanistan. The actual mathematical processes are quite complex but the equivalent formula for the direction of the qibla using modern notation is the following:
q = arctan[(sinΔλ)/(cosφd*tanφm-sinφd*cosΔλ)]
Where, Δλ = λm – λd is the difference in longitude between Mecca and the desired location.
φd is the latitude of the desired location
φm is the latitude of Mecca
It is evident that to use this method one must have ways of finding the latitudes of both Mecca and the desired location and also the difference in longitude of the two locations.
Finding the latitude of a location is relatively easy and methods of determining it were known to the ancient Greeks. One simple way is to measure the zenith distance of the Sun at the equinox (when day and night have equal duration) at local noon (i.e. when the Sun is directly to the South). The latitude of the location is then simply equal to this zenith distance.
Determining longitude is a much more difficult problem that was not solved until several hundred years later when the Englishman John Harisson developed an accurate clock. However, it is evident from the formulae presented above, that it is only necessary to know the difference in longitude, Δλ, to determine the direction to Mecca. Al-Biruni tells us that the best way to do this at his time, was to use the method of lunar eclipses, the one Ptolemy also used many hundred years before him.
Implementation in Stellarium
We will use the lunar eclipse method to find the difference in longitude between Ghazni and Mecca.
Start Stellarium and in the Date/Time Window, set the date to:
1019 / 09 / 17.
Next, set the location in the Location Window to Ghazni in Afghanistan. Using the Date/Time Window, set the time to 2:15 am.
You must now look closely at the Moon, to do this you should click on it and then press the Page Up key to zoom in. Progress the time until you observe the beginning of the lunar eclipse.
What is the local time at Ghazni when the lunar eclipse begins, i.e. when the Moon first becomes starts to enter the shadow of the Earth?
Set the location in the Location Window to Mecca in Saudi Arabia.
Determine the local time at which the lunar eclipse commences in Mecca. From this and your measurement in Ghazni, determine the difference in time and hence the difference in longitude between the two cities.
Now we must find the latitude of the two cities using one of the methods of the ancient astronomers.
We must perform our measurements at the equinox.
Start Stellarium and in the Date/Time Window, set the date to:
1119 / 3 / 15
This was the date of the spring equinox at that year.
To perform the experiment correctly we must find the local noon in Alexandria, i.e. the exact time when the Sun’s altitude is at its greatest, which for the Northern Hemisphere is when it is located exactly South. This is when the Sun’s azimuth is 180 degrees.
Vary the time (round about midday) to find the local noon at Mecca at the spring equinox of 1119 AD. Record the altitude of the Sun at this point. Next determine the zenith distance of the Sun.
θ = 90 – Altitude degrees.
This is then the latitude of Mecca. You can check it against the latitude given by Stellarium.
Next, set the location in the Location Window to Ghazni. Repeat the above procedure to obtain the latitude of Ghazni. You can again check it against the value given by Stellarium.
Let us now use all the information obtained to find the direction of the qibla from Ghazni.
First use the approximate formula:
q = arctan(Δλ/Δφ)
Note the value of q found.
It is important that you use the following conventions: the sign of λ is positive for locations east of Greenwich and negative for locations to the west and the sign of φ is positive when north and negative when south of the equator. It is also important to place the angle q in the right quadrant. For example, if both the numerator and denominator of the quotient are negative, this means that both the sine and cosine are negative, and the angle q must lie in the third quadrant.
Next, with the same conventions as above, use the more accurate formula based on spherical trigonometry:
q = arctan[(sinΔλ)/(cosφd*tanφm-sinφd*cosΔλ)]
Note the difference between the approximate and exact results.
Many scholars worked on this problem, including one of the most prominent scientists of that era, the Iranian Abu Rayhan al-Biruni (973 – after 1050 CE). Al – Biruni studied almost all fields of science including mathematics, physics and astronomy. One of his most important works was the “Taḥdid nihāyāt al-amākin li-taṣḥīḥ masāfāt al-masākin” (“Determination of the Coordinates of Places for the Correction of Distances Between Cities”). In it he detailed all that one needed to know about determining longitudes and latitudes on land and provided a novel solution for determining the circumference of the Earth. He also came up with ingenious solutions to the spherical trigonometric problem of determining the direction of Mecca from Ghazni, the city in Afghanistan. The actual mathematical processes are quite complex but the equivalent formula for the direction of the qibla using modern notation is the following:
q = arctan[(sinΔλ)/(cosφd*tanφm-sinφd*cosΔλ)]
Where, Δλ = λm – λd is the difference in longitude between Mecca and the desired location.
φd is the latitude of the desired location
φm is the latitude of Mecca
It is evident that to use this method one must have ways of finding the latitudes of both Mecca and the desired location and also the difference in longitude of the two locations.
Finding the latitude of a location is relatively easy and methods of determining it were known to the ancient Greeks. One simple way is to measure the zenith distance of the Sun at the equinox (when day and night have equal duration) at local noon (i.e. when the Sun is directly to the South). The latitude of the location is then simply equal to this zenith distance.
Determining longitude is a much more difficult problem that was not solved until several hundred years later when the Englishman John Harisson developed an accurate clock. However, it is evident from the formulae presented above, that it is only necessary to know the difference in longitude, Δλ, to determine the direction to Mecca. Al-Biruni tells us that the best way to do this at his time, was to use the method of lunar eclipses, the one Ptolemy also used many hundred years before him.
Implementation in Stellarium
We will use the lunar eclipse method to find the difference in longitude between Ghazni and Mecca.
Start Stellarium and in the Date/Time Window, set the date to:
1019 / 09 / 17.
Next, set the location in the Location Window to Ghazni in Afghanistan. Using the Date/Time Window, set the time to 2:15 am.
You must now look closely at the Moon, to do this you should click on it and then press the Page Up key to zoom in. Progress the time until you observe the beginning of the lunar eclipse.
What is the local time at Ghazni when the lunar eclipse begins, i.e. when the Moon first becomes starts to enter the shadow of the Earth?
Set the location in the Location Window to Mecca in Saudi Arabia.
Determine the local time at which the lunar eclipse commences in Mecca. From this and your measurement in Ghazni, determine the difference in time and hence the difference in longitude between the two cities.
Now we must find the latitude of the two cities using one of the methods of the ancient astronomers.
We must perform our measurements at the equinox.
Start Stellarium and in the Date/Time Window, set the date to:
1119 / 3 / 15
This was the date of the spring equinox at that year.
To perform the experiment correctly we must find the local noon in Alexandria, i.e. the exact time when the Sun’s altitude is at its greatest, which for the Northern Hemisphere is when it is located exactly South. This is when the Sun’s azimuth is 180 degrees.
Vary the time (round about midday) to find the local noon at Mecca at the spring equinox of 1119 AD. Record the altitude of the Sun at this point. Next determine the zenith distance of the Sun.
θ = 90 – Altitude degrees.
This is then the latitude of Mecca. You can check it against the latitude given by Stellarium.
Next, set the location in the Location Window to Ghazni. Repeat the above procedure to obtain the latitude of Ghazni. You can again check it against the value given by Stellarium.
Let us now use all the information obtained to find the direction of the qibla from Ghazni.
First use the approximate formula:
q = arctan(Δλ/Δφ)
Note the value of q found.
It is important that you use the following conventions: the sign of λ is positive for locations east of Greenwich and negative for locations to the west and the sign of φ is positive when north and negative when south of the equator. It is also important to place the angle q in the right quadrant. For example, if both the numerator and denominator of the quotient are negative, this means that both the sine and cosine are negative, and the angle q must lie in the third quadrant.
Next, with the same conventions as above, use the more accurate formula based on spherical trigonometry:
q = arctan[(sinΔλ)/(cosφd*tanφm-sinφd*cosΔλ)]
Note the difference between the approximate and exact results.