Estimating the distance to the Moon (Hipparchus)
Activity objectives
Background
Hipparchus (190 – 120 BCE) was a Greek astronomer, geographer, and mathematician, born in the ancient city of Nicaea (modern day Turkey) and like Posidonius, also spent time on the island of Rhodes. In astronomy he is known as the greatest star observer of antiquity as he catalogued the position and brightness of hundreds of stars. Hipparchus was also the first to deduce the precession of the equinoxes (the slight wobble of the Earth’s rotational axis) and estimated the duration of the solar year with amazing accuracy for his time. For these and many other achievements he is regarded by many as the greatest astronomer of antiquity. Apart from his advances in astronomy he is also famous for his discovery of trigonometry.
- Learn about Hipparchus, one of the greatest astronomers of antiquity
- Obtain an understanding of solar eclipses
- Obtain an understanding of the parallax phenomenon
- Use the lunar parallax to estimate the distance to the Moon
- Use Stellarium to replicate the measurement of the distance to the Moon
- Become aware of the errors and limitations approximating the method of Hipparchus
Background
Hipparchus (190 – 120 BCE) was a Greek astronomer, geographer, and mathematician, born in the ancient city of Nicaea (modern day Turkey) and like Posidonius, also spent time on the island of Rhodes. In astronomy he is known as the greatest star observer of antiquity as he catalogued the position and brightness of hundreds of stars. Hipparchus was also the first to deduce the precession of the equinoxes (the slight wobble of the Earth’s rotational axis) and estimated the duration of the solar year with amazing accuracy for his time. For these and many other achievements he is regarded by many as the greatest astronomer of antiquity. Apart from his advances in astronomy he is also famous for his discovery of trigonometry.
Hipparchus Observing from Alexandria: Taken from https://commons.wikimedia.org/wiki/File:Observatory_in_Alexandria_at_the_Time_of_Hipparchus.jpg
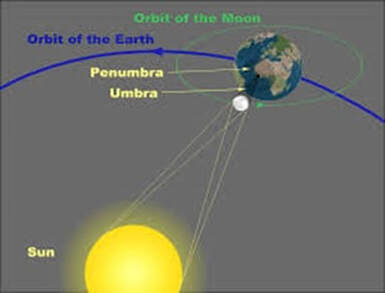
Hipparchus used observations from a total eclipse of the Sun to estimate the distance of the Moon from the Earth. The eclipse he used was total at the Hellespont (the narrow strait that separates the European and Asian parts of Turkey) but only part of the Sun was seen covered from Alexandria, in Egypt.
For a total eclipse of the Sun - Moon - Earth are aligned. The Sun itself is so distant that when viewed from anywhere on Earth, it covers practically the same patch of the sky, with an angular width of about 0.5°.
Hipparchus used observations from a total eclipse of the Sun to estimate the distance of the Moon from the Earth. The eclipse he used was total at the Hellespont (the narrow strait that separates the European and Asian parts of Turkey) but only part of the Sun was seen covered from Alexandria, in Egypt.
For a total eclipse of the Sun - Moon - Earth are aligned. The Sun itself is so distant that when viewed from anywhere on Earth, it covers practically the same patch of the sky, with an angular width of about 0.5°.
Geometry of solar eclipse: Taken from: http://www.planetary.org/multimedia/space-images/charts/geometry-of-a-total-solar.html
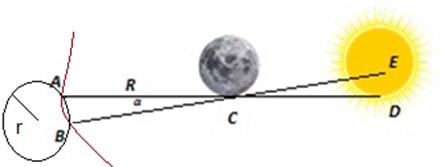
Hipparchus concentrated on point C at the edge of the Moon, which during totality, when viewed from the Hellespont (point A), just overlapped point D on the edge of the Sun.
Hipparchus concentrated on point C at the edge of the Moon, which during totality, when viewed from the Hellespont (point A), just overlapped point D on the edge of the Sun.
Simplification of the method of Hipparchus for estimating the circumference of the Earth
Viewed from Alexandria (point B), the point C only overlapped point E on the Sun, about x solar diameters short of the edge, which was why the eclipse there was not total. The number x (smaller than 1), denotes the fraction of the Sun that remains visible. So, for example if 20% of the Sun remains visible then x is 0.2.
A fraction x of the diameter of the Sun covers an angle of 0.5x in the sky (since the angular size of the Sun as viewed from the Earth is approximately 0.5 degrees, the same as that of the Moon). So, the small angle α between the two directions is approximately 0.5x degrees. Note that in astronomy this angle is called the parallax of the edge of the Moon as viewed from the above two locations.
Hipparchus knew the latitudes of Hellespont and Alexandria. He also assumed that Alexandria is exactly due south. Furthermore, from simple geometry:
AB = 2πr(Δφ/360)
where Δφ is the difference in latitude between the Hellespont and Alexandria and r is the radius of the Earth.
The points A, B are also located on another circle which has the Moon at its centre. The radius in that case is the distance R to the Moon, and because the arc AB covers 0.5x degrees, we get:
AB = 2πR(0.5x/360)
Of course, each of the two arcs AB expressed in the above equations is measured along a different circle, with a different radius (and the two circles curve in opposite ways). Since, however, in both cases AB covers only a small part of the circle, as an approximation we may regard each of the arcs as equal to the chord AB. This assumption allows us to make the two expressions equal:
2πr(Δφ/360) = 2πR(0.5x/360)
This in turn gives,
R/r = Δφ/(0.5x)
Therefore, by knowing the difference in latitude Δφ and also the fraction x of the Sun that is still visible, we can estimate the distance to the Moon in terms of the radius of the Earth.
It is important to note that the approximate geometric method described here is a very simplified version of the geometric calculations that Hipparchus himself will have used (for example it assumes that the Sun is directly overhead when the eclipse occurs, which is not the case). His more sophisticated calculations yielded more accurate results than those that we will obtain but the essence of the method remains the same.
Implementation in Stellarium
According to most scholars (although opinions do vary), Hipparchus used for his measurements the solar eclipse which took place on the 14th of March, 190 BCE (he must have learned of the measurements from earlier sources). Start Stellarium and in the Time/Date Window set the date to:
-189 / 3 / 14.
Next, set the location in the Location Window to Iznik in modern day Turkey. This is where the birthplace of Hipparchus (the ancient city of Nicaea) stood on the Hellespont strait. Note the latitude of the location.
Set the local time to around 7:25 am. Let the time run and verify that a total solar eclipse did occur on this day and could be viewed from the Hellespont. Once again you must zoom in using the Page Up key.
Now change the location to Alexandria in Egypt, note the latitude and set the local time to 7:00 am. Observe the partial solar eclipse and try to make an estimate of the minimum percentage of the Sun that is visible as viewed from this location, i.e. the number x described in the calculations above.
Use the procedure described above to estimate the distance to the Moon assuming that the radius of the Earth is 6,371 km. Compare this to the actual distance and comment on sources of error. Combine your result with that of the first experiment of Aristarchus to obtain the distance to the Sun in kilometers.
Viewed from Alexandria (point B), the point C only overlapped point E on the Sun, about x solar diameters short of the edge, which was why the eclipse there was not total. The number x (smaller than 1), denotes the fraction of the Sun that remains visible. So, for example if 20% of the Sun remains visible then x is 0.2.
A fraction x of the diameter of the Sun covers an angle of 0.5x in the sky (since the angular size of the Sun as viewed from the Earth is approximately 0.5 degrees, the same as that of the Moon). So, the small angle α between the two directions is approximately 0.5x degrees. Note that in astronomy this angle is called the parallax of the edge of the Moon as viewed from the above two locations.
Hipparchus knew the latitudes of Hellespont and Alexandria. He also assumed that Alexandria is exactly due south. Furthermore, from simple geometry:
AB = 2πr(Δφ/360)
where Δφ is the difference in latitude between the Hellespont and Alexandria and r is the radius of the Earth.
The points A, B are also located on another circle which has the Moon at its centre. The radius in that case is the distance R to the Moon, and because the arc AB covers 0.5x degrees, we get:
AB = 2πR(0.5x/360)
Of course, each of the two arcs AB expressed in the above equations is measured along a different circle, with a different radius (and the two circles curve in opposite ways). Since, however, in both cases AB covers only a small part of the circle, as an approximation we may regard each of the arcs as equal to the chord AB. This assumption allows us to make the two expressions equal:
2πr(Δφ/360) = 2πR(0.5x/360)
This in turn gives,
R/r = Δφ/(0.5x)
Therefore, by knowing the difference in latitude Δφ and also the fraction x of the Sun that is still visible, we can estimate the distance to the Moon in terms of the radius of the Earth.
It is important to note that the approximate geometric method described here is a very simplified version of the geometric calculations that Hipparchus himself will have used (for example it assumes that the Sun is directly overhead when the eclipse occurs, which is not the case). His more sophisticated calculations yielded more accurate results than those that we will obtain but the essence of the method remains the same.
Implementation in Stellarium
According to most scholars (although opinions do vary), Hipparchus used for his measurements the solar eclipse which took place on the 14th of March, 190 BCE (he must have learned of the measurements from earlier sources). Start Stellarium and in the Time/Date Window set the date to:
-189 / 3 / 14.
Next, set the location in the Location Window to Iznik in modern day Turkey. This is where the birthplace of Hipparchus (the ancient city of Nicaea) stood on the Hellespont strait. Note the latitude of the location.
Set the local time to around 7:25 am. Let the time run and verify that a total solar eclipse did occur on this day and could be viewed from the Hellespont. Once again you must zoom in using the Page Up key.
Now change the location to Alexandria in Egypt, note the latitude and set the local time to 7:00 am. Observe the partial solar eclipse and try to make an estimate of the minimum percentage of the Sun that is visible as viewed from this location, i.e. the number x described in the calculations above.
Use the procedure described above to estimate the distance to the Moon assuming that the radius of the Earth is 6,371 km. Compare this to the actual distance and comment on sources of error. Combine your result with that of the first experiment of Aristarchus to obtain the distance to the Sun in kilometers.