Estimating the distance to the Sun (Aristarchus)
Activity objectives
Background
Aristarchus (310 - 230 BCE) was an ancient Greek astronomer and mathematician born on the Greek island of Samos. He is famous for being the first scientist to support the heliocentric model of the solar system, i.e. that the Earth and planets revolve around the Sun. Unfortunately, his theory was not generally accepted and the geocentric model (by which the Sun and planets revolve around the Earth) was the prevailing theory until the 16th century CE when the Polish astronomer Nicolaus Copernicus revived and expanded on the ideas first presented by Aristarchus.
- Learn about Aristarchus a great astronomer of antiquity
- Obtain an understanding of the phases of the Moon
- Use simple geometric methods to estimate the relative distance of the Sun
- Use Stellarium to replicate the measurement of the relative distance of the Sun
- Become aware of the errors and limitations of the method of Aristarchus
Background
Aristarchus (310 - 230 BCE) was an ancient Greek astronomer and mathematician born on the Greek island of Samos. He is famous for being the first scientist to support the heliocentric model of the solar system, i.e. that the Earth and planets revolve around the Sun. Unfortunately, his theory was not generally accepted and the geocentric model (by which the Sun and planets revolve around the Earth) was the prevailing theory until the 16th century CE when the Polish astronomer Nicolaus Copernicus revived and expanded on the ideas first presented by Aristarchus.
Aristarchus: Taken from https://commons.wikimedia.org/wiki/File:Aristarchos_von_Samos_(Denkmal).jpeg
Aristarchus may be famous for his heliocentric model but in his work “On the Sizes and Distances of the Sun and Moon”, he also presented a series of calculations which although due to his lack of accurate scientific instruments were prone to relatively large errors, were immensely impressive in their theoretical make up. In this and in the next activity, we will replicate two of his brilliant experiments.
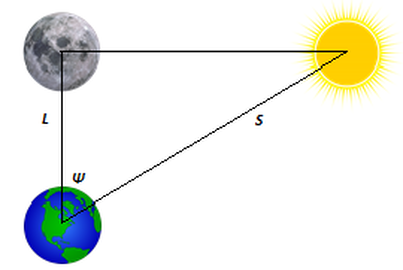
With his first experiment Aristarchus estimated the distance between the Earth and the Sun in terms of distance from the Earth of the Moon. His idea was beautifully simple. As seen in the following figure, when the Moon is at the quarter Moon phase (i.e. when it seems half lit to us), the Sun – Moon – Earth angle is a right angle. So, by determining the Moon – Earth – Sun angle (let us call it ψ), we can find the distance of the Sun from the Earth from:
cos ψ = L/S
Aristarchus may be famous for his heliocentric model but in his work “On the Sizes and Distances of the Sun and Moon”, he also presented a series of calculations which although due to his lack of accurate scientific instruments were prone to relatively large errors, were immensely impressive in their theoretical make up. In this and in the next activity, we will replicate two of his brilliant experiments.
With his first experiment Aristarchus estimated the distance between the Earth and the Sun in terms of distance from the Earth of the Moon. His idea was beautifully simple. As seen in the following figure, when the Moon is at the quarter Moon phase (i.e. when it seems half lit to us), the Sun – Moon – Earth angle is a right angle. So, by determining the Moon – Earth – Sun angle (let us call it ψ), we can find the distance of the Sun from the Earth from:
cos ψ = L/S
Method of Aristarchus for estimating the distance to the Sun
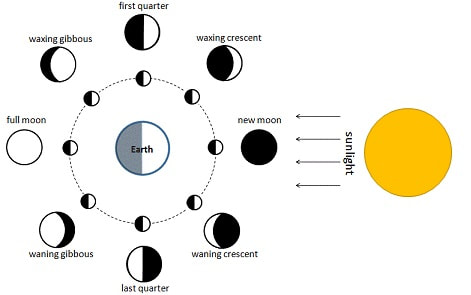
To obtain a better understanding you can view the phases of the Moon in the following diagram. Note how the Sun, Earth and Moon form a right-hand angle when the Moon is at quarter phase.
To obtain a better understanding you can view the phases of the Moon in the following diagram. Note how the Sun, Earth and Moon form a right-hand angle when the Moon is at quarter phase.
Phases of the Moon: Adapted from https://simple.m.wikipedia.org/wiki/File:Moon_Phase_Diagram_for_Simple_English_Wikipedia.GIF
Implementation in Stellarium
Note: To complete this activity you must have the Angle Measure plugin enabled. To enable the Angle Measure plugin, you must first go to the Configuration Window and to Plugins, locate the plugin and select Load at Startup. You will need to restart Stellarium for the plugin to work.
Start Stellarium and in the Date/Time Window, set the date to:
-280 / 10 / 15 (any other day when the Moon is half illuminated will do).
Next, set the location in the Location Window, to Athens in Greece (Aristarchus may have spent some of his time there). Set the local time to around 10 am and find and freeze the exact moment when the Moon is illuminated by 50%. You can find the illumination of the Moon by clicking on it and checking the information provided, it is towards the end of the list of info.
Use the Angle Measure plugin to measure the angular distance between the Moon and the Sun at this moment, this is the angle ψ.
Use the cosine formula provided above to find the distance of the Sun from the Earth in terms of the distance of the Moon from the Earth. Compare to the result accepted nowadays and on possible sources of error.
Add or subtract 0.5 degree to your angular measurement result and see what effect it has on your final result. This will give you an understanding on how difficult the measurement was for Aristarchus and why his final result was prone to error.
Note that this experiment provides us with an estimate of the distance of the Sun in terms of the distance to the Moon. In following activities, we will calculate the actual distance to the Moon and therefore it will be possible to produce an absolute value for the distance to the Sun.
Implementation in Stellarium
Note: To complete this activity you must have the Angle Measure plugin enabled. To enable the Angle Measure plugin, you must first go to the Configuration Window and to Plugins, locate the plugin and select Load at Startup. You will need to restart Stellarium for the plugin to work.
Start Stellarium and in the Date/Time Window, set the date to:
-280 / 10 / 15 (any other day when the Moon is half illuminated will do).
Next, set the location in the Location Window, to Athens in Greece (Aristarchus may have spent some of his time there). Set the local time to around 10 am and find and freeze the exact moment when the Moon is illuminated by 50%. You can find the illumination of the Moon by clicking on it and checking the information provided, it is towards the end of the list of info.
Use the Angle Measure plugin to measure the angular distance between the Moon and the Sun at this moment, this is the angle ψ.
Use the cosine formula provided above to find the distance of the Sun from the Earth in terms of the distance of the Moon from the Earth. Compare to the result accepted nowadays and on possible sources of error.
Add or subtract 0.5 degree to your angular measurement result and see what effect it has on your final result. This will give you an understanding on how difficult the measurement was for Aristarchus and why his final result was prone to error.
Note that this experiment provides us with an estimate of the distance of the Sun in terms of the distance to the Moon. In following activities, we will calculate the actual distance to the Moon and therefore it will be possible to produce an absolute value for the distance to the Sun.